|
|
|
W h o W e A r e a n d W h a t W e D o
1. Human Knowledge and Mathematical Modeling
2. A Brief Overview of Our Research
3. Research Projects and Topics of Interest
1. Human Knowledge and Mathematical Modeling
We are a multidisciplinary group based at the M²NeT Lab, Waterloo, Canada. At the M²NeT Lab, we focus on the development and analysis of mathematical models for multiscale coupled systems and phenomena. In this context, we deal with a range of cutting edge problems at the interface of mathematical sciences and such disciplines as physics and mechanics, nanoscience and nanotechnology, engineering and materials science, biological sciences and medicine. Mathematical modeling is a universal tool of modern science and engineering, a tool that is becoming increasingly indispensable in virtually all the areas of human endeavors. Mathematical models provide a ubiquitous framework for scientific progress, the development of new technologies, sustainable development of society, and the ever-expanding boundaries of human knowledge. They also serve as a natural safeguard against narrow specialization which, according to Einstein, is damaging to scientific progress and the true spirit of research.
“The area of scientific knowledge has been enormously extended, and theoretical knowledge has become vastly more profound in every department of science. But the assimilative power of the human intellect is and remains strictly limited. Hence it was inevitable that the activity of the individual investigator should be confined to a smaller and smaller section of human knowledge. Worse still, this specialization makes it increasingly difficult to keep even our general understanding of science as a whole, without which the true spirit of research is inevitably handicapped, in step with scientific progress.” (Albert Einstein)
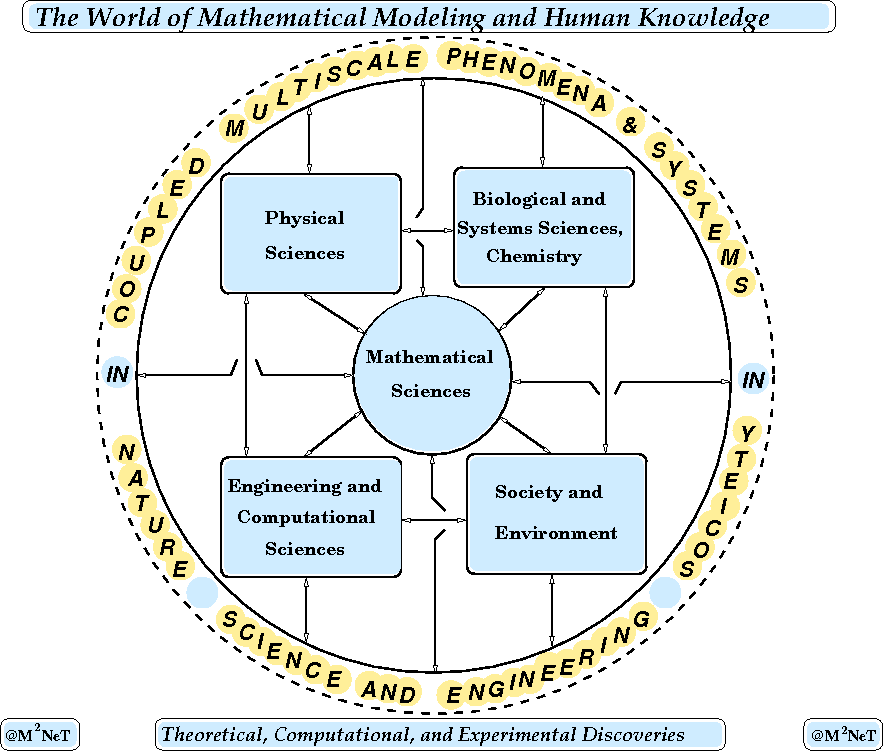
We believe that the true spirit of research and the key fundamentals in our general understanding of science as a whole as well as in our further progress in specific areas of science, engineering, and other areas of human endevour will increasingly rely on our progress in the field of mathematical modeling. At the M²NeT Lab, our view on the place of mathematical modeling in the dynamic process of expanding the boundaries of human knowledge is schematically presented below.
2. A Brief Overview of Our Research
Most of the problems we deal with lie at the interface between science & engineering and mathematics where the development and application of efficient mathematical modeling tools and techniques is a key to success. This requires addressing both fundamental and applied issues.
In our group, we focus on the development of mathematical models and computational techniques for the following main areas:
Many problems we deal with are based on models that can be written in the form of partial differential equations. Since systems and phenomena we study usually involve interactions of processes over a range of spatial and temporal scales, such problems are often multiscale in their nature. Many such problems are coupled problems and in the context of physical and engineering applications are often termed as multi-physics. The term "coupled", however, is more generic as it is applied also to problems in bilogy, medicine, and other fields in science & engineering. Some of the models we deal with are non-local and therefore can be represented by integro-differential equations (e.g., problems involving collisions of many particles or interactions of many bodies provide typical examples), while others are essentially discrete models. Our interests include also non-equilibrium processes and systems far from their equilibrium. In a number of situations we have to take into account incompleteness of the information about the system or phenomenon we study which lead to stochastic models and probabilistic approaches. The models we deal with covers the spatial scales from nano to macro levels as well as a range of time scales.
In all the above areas, the solution of vast majority of problems is not amenable to analytical treatments and the development of efficient numerical methodologies is required. Computational science and engineering relies on the development of mathematical modeling tools, and in this context our interests include also computational and mathematical physics, biological and life science applications, and engineering mathematics. Engineering and science applications enrich applied mathematics and the interface between these disciplines represent the core of of our research activities. Today, this interface encompasses some of the most challenging problems of modern science and technology. This trend will persist into the future, bringing exciting new opportunities for those researchers who are able to work in an interdisciplinary environment. Such opportunities exist in our group for those students who are keen on facing these challenges in their future careers for the benefit of our society. If you are a student, in particular a potential graduate student, or a researcher who is interested in working/collaborating with us on one of our current or emerging projects, please contact us.
3. Research Projects and Topics of Interest
The following projects represent some of the areas of our research contributions. The research has been supported by funding agencies in Europe, Australia, and North America. These projects are of continuing interest, although they may not be listed here in the order of our current priorities. The list of downloadable papers is available from the bar menu above or follow this link. Inquiries, regarding these and our new emerging projects, are welcome.
Follow this link for a list of collaborators.
|
|
|
|
|